Contact Dynamics
Simulating multibody systems with frictional contact is crucial in robotics, particularly for training robotic systems. This blog introduces some fundamental concepts of contact modeling. Let’s consider the contact between the point foot of a quadruped and the ground. We define the gap function $\phi(q)$ as the signed distance between the point foot and the ground, where $q$ represents the generalized positions.
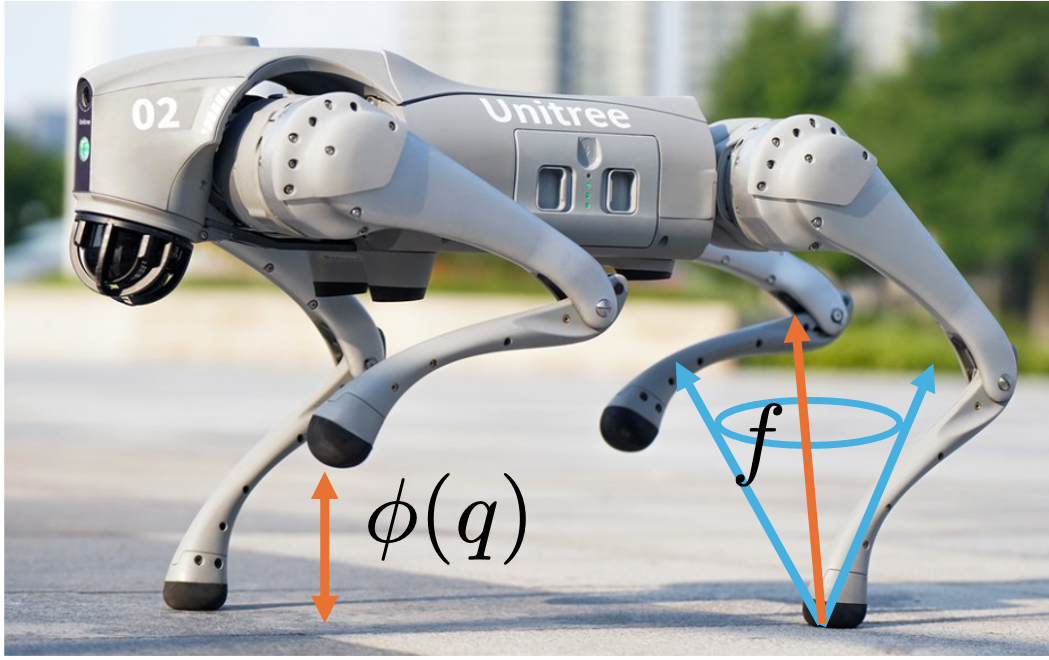
The contact force $f$, expressed in the local frame, consists of the tangential component $f_T$ and the normal component $f_N$. The magnitude and direction of the contact force are not arbitrary. As you may have heard, the contact force should lie within the so-called friction cone. One of our main goals is to identify the constraints related to this force, and we will dive into those details later. But for now, let’s step back and look at the bigger picture — what exactly are we trying to compute when simulating a single time step? We assume that you are familiar with the following equations of motion:
\[M (q)\dot{v} = \tau - h(q, v) + J^\top (q) \boldsymbol{f},\]where $v$ is the generalized velocity, $M(q)$ denotes the joint space inertia matrix, $h(q, v)$ accounts for the centrifugal and Coriolis effects, and $\tau$ is the actuation torque. The collection of contact forces is denoted as $\boldsymbol{f} \in \mathbb{R}^{3 N_c}$, where $N_c$ is the number of contacts that the robot makes at the current time instance. $J(q)$ represents the Jacobian, which maps the generalized velocity to the collection of contact velocities expressed in the local contact frames. To discretize the system, we adopt the semi-implicit Euler integration scheme:
\[M(q_t)(v_{t+1} - v_t) = \Delta t\left(\tau_t - h(q_t, v_t)\right) + J(q_t)^\top \boldsymbol{\lambda},\]where $\boldsymbol{\lambda}$ is the collection of contact impulses. Our goal is to compute $\boldsymbol{\lambda}$ and $v_{t+1}$, and then use $v_{t+1}$ to obtain $q_{t+1}$. Now, it is time to discuss the constraints on contact forces/impulses.
-
First, the normal component of the contact force should be nonnegative, i.e., $f_N \geq 0$. This means the environment can push against the feet of a quadruped, but it cannot pull them toward the ground.
-
The signed distance is expected to be nonnegative as well, i.e., $\phi(q) \geq 0$.
-
The signed distance and contact force cannot be nonnull at the same time, i.e., $\lambda_N\, \phi(q) = 0$.
The conditions above are known as the so-called Signorini condition, which can be rewritten in a compact form:
\[0 \leq f_{N} \perp \phi(q) \geq 0.\]We discretize the condition to make it easier to handle numerically. The signed distance can be approximately computed by
\[\begin{aligned} \phi(q_{t+1}) \approx \phi(q_{t}) + \Delta t c_{N, t+1} &\geq 0 \\ \frac{1}{\Delta t} \phi(q_{t}) + c_{N, t+1} &\geq 0, \end{aligned}\]where $c = (c_T, c_N) \in \mathbb{R}^3$ denotes the contact velocity expressed in the contact frame. The relationship between the i-th contact velocity and the generalized velocity is given by
\[c_{i, t+1} = J_i(q_t) v_{t+1}.\]Replacing $f_N$ with $\lambda_N$, we rewrite the Signorini condition as
\[\begin{equation} \label{eq:comp_constr} 0 \leq \lambda_{N} \perp \left( \frac{1}{\Delta t} \phi(q_{t}) + c_{N, t+1} \right) \geq 0. \end{equation}\]Let’s continue to introduce the constraints on forces/impulses.
- One common friction model follows Coulomb’s law for dry friction. Mathematically, this law suggests that the contact force should stay inside the friction cone:
where $\mu > 0$ is the coefficient of friction.
- When sliding occurs, the tangential component $\lambda_T \in \mathbb{R}^2$ should follow the maximum dissipation principle:
To reach the minimum, the friction impulse $\lambda_T$ acts in the opposite direction of the sliding velocity, i.e., $-\frac{c_T}{\Vert c_T \Vert_2}$, with a magnitude of $\mu \lambda_N$. As a result, the expression for $\lambda_T$ is then
\[\begin{equation} \label{eq:mdp} \lambda_T = - \mu \lambda_N \dfrac{c_{T, t+1}}{\Vert c_{T, t+1} \Vert_2} \quad \text{if}\; \Vert c_{T, t+1} \Vert_2 > 0 \; \text{and} \; \left( \dfrac{1}{\Delta t} \phi(q_{t}) + c_{N, t+1} \right) = 0. \end{equation}\]The two conditions, $ \Vert c_{T, t+1} \Vert_2 > 0$ and $\left( \frac{1}{\Delta t} \phi(q_{t}) + c_{N, t+1} \right) = 0$, indicates that the contact is undergoing sliding motion.
With all conditions established, we now apply them to various contact situations. There are three typical contact situations: take-off, sticking, and sliding.
- Take-off (Loss of Contact)
In this situation, the contact is breaking, i.e., $\left( \frac{1}{\Delta t} \phi(q_{t}) + c_{N, t+1} \right) > 0$. According to \eqref{eq:comp_constr} and \eqref{eq:f_cone}, the contact force should be null.
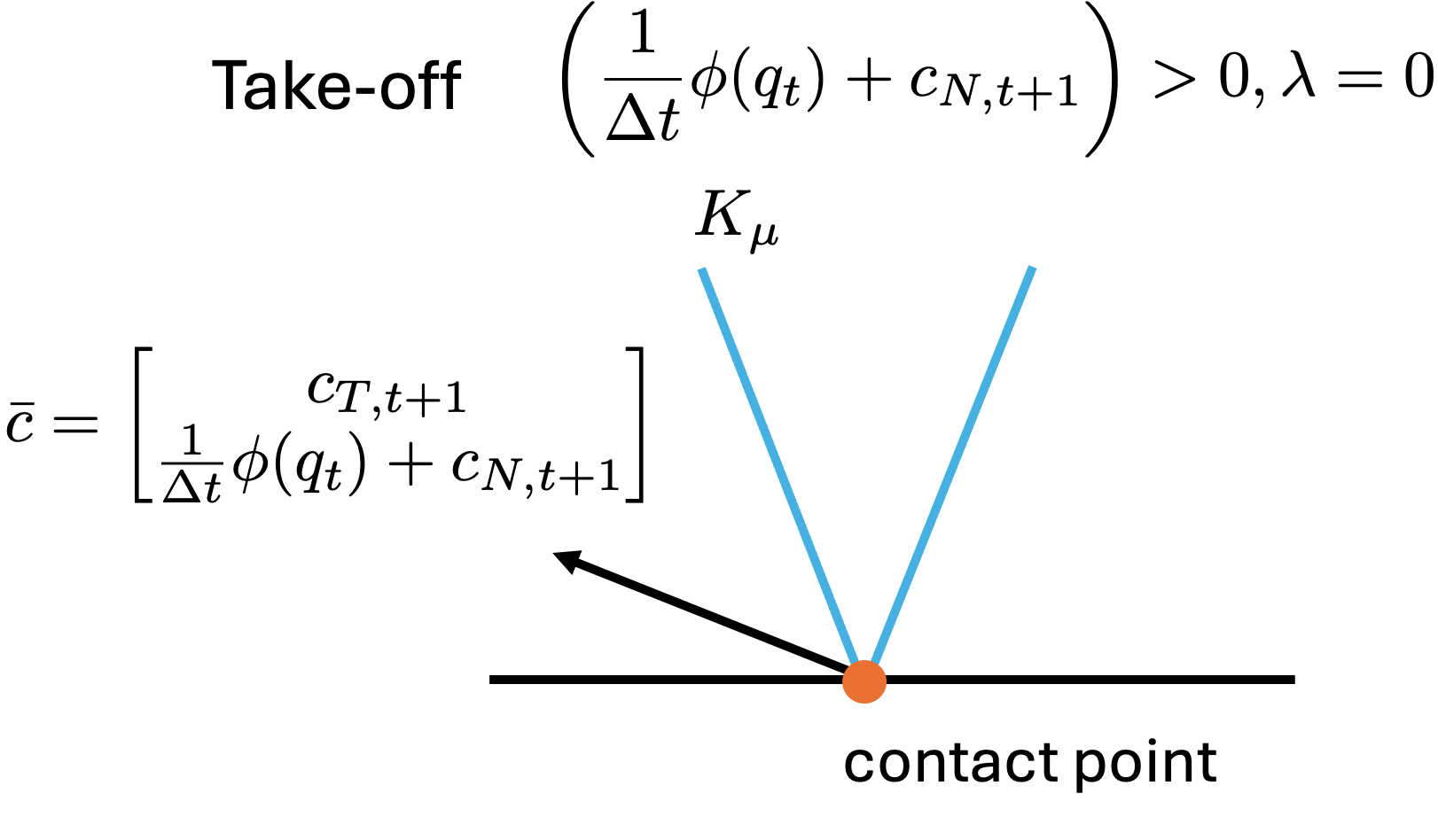
When contact is maintained, i.e., $\left( \frac{1}{\Delta t} \phi(q_{t}) + c_{N, t+1} \right) = 0$, there are two possible cases to consider: sticking and sliding.
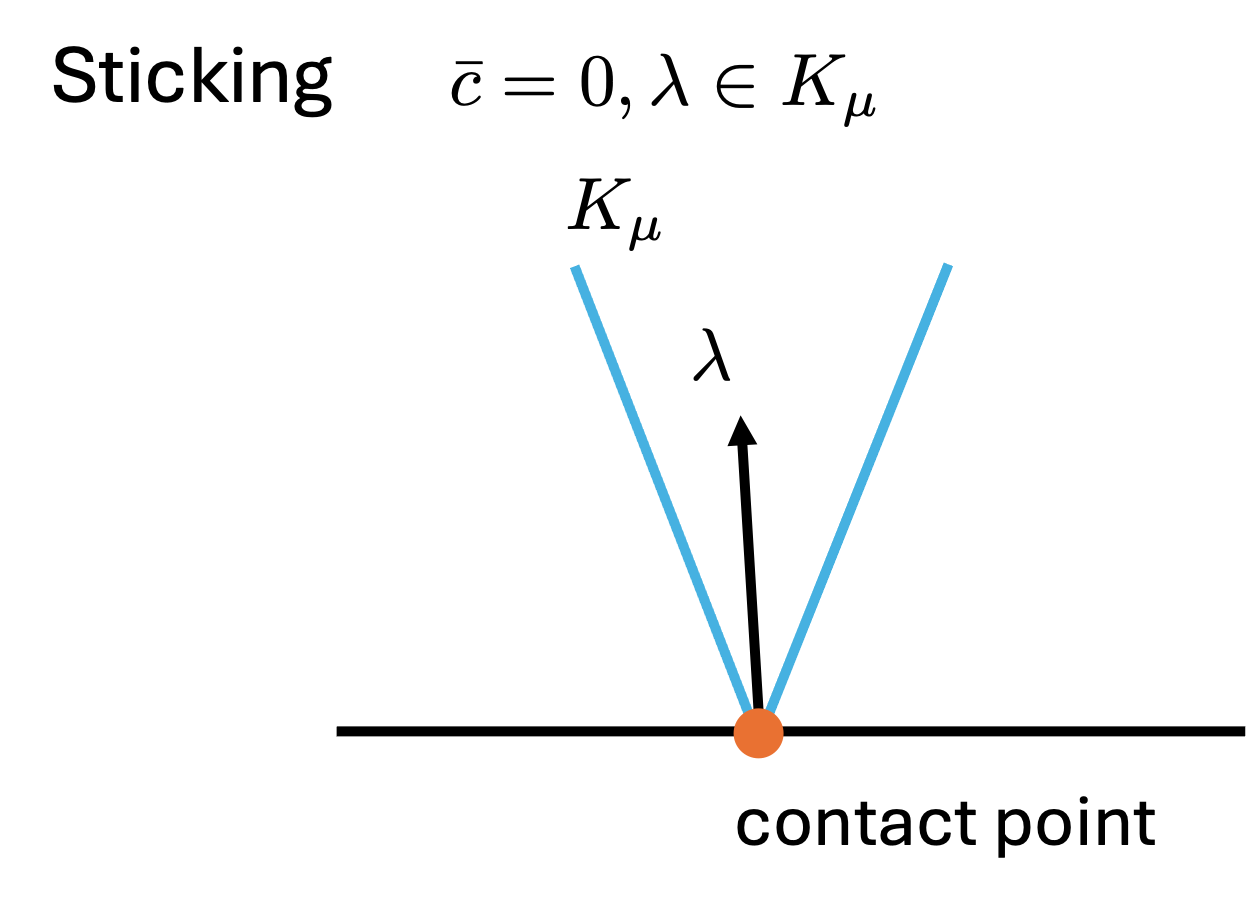
- Sticking (Static Contact)
In this situation, the tangential contact velocity is zero and the contact force lies inside the friction cone.
- Sliding (Dynamic Contact with Friction)
In this case, according to \eqref{eq:mdp}, the tangential contact velocity is strictly positive and the contact force reaches the boundary of the friction cone.
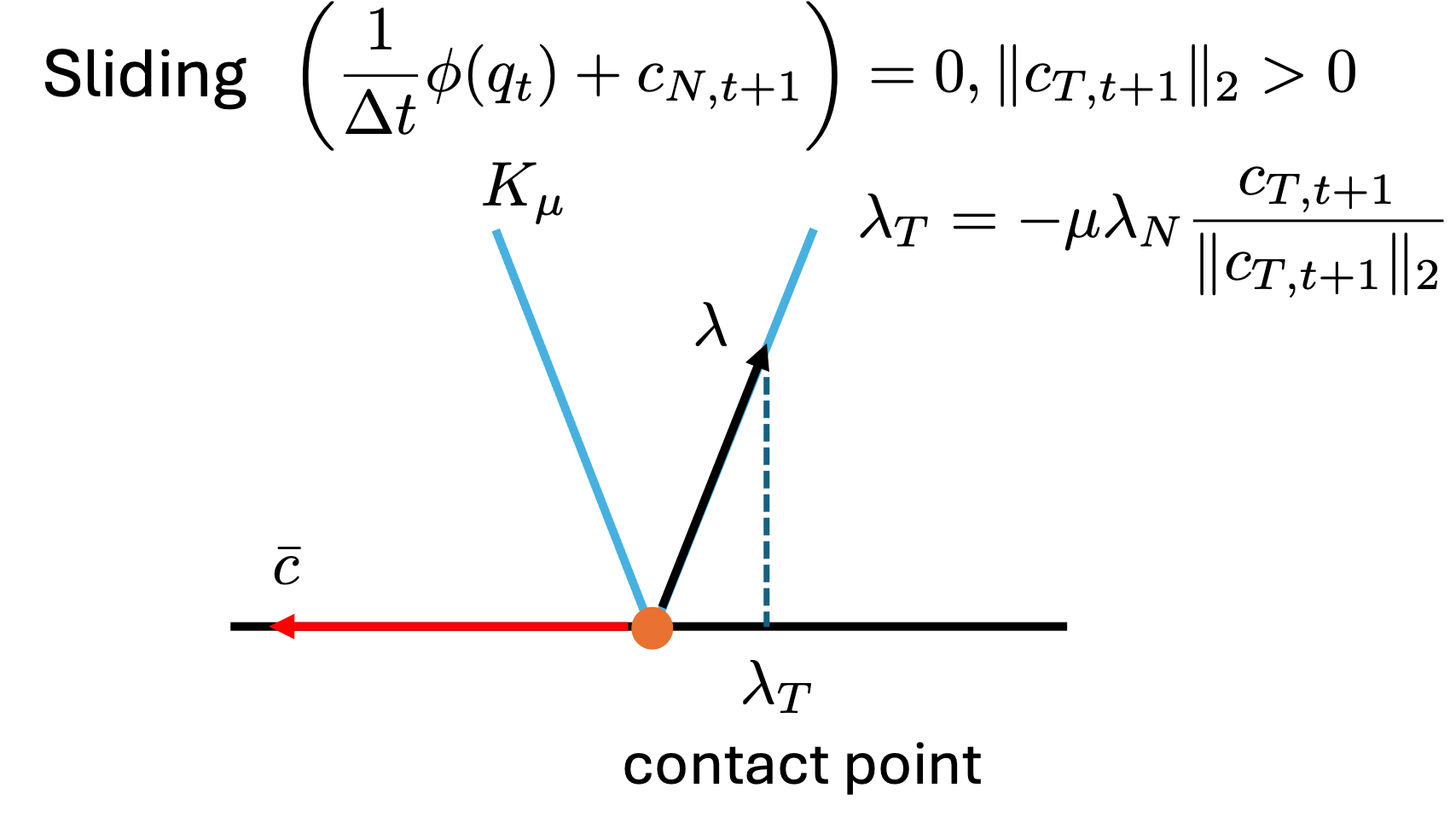
Unfortunately, we cannot obtain a compact formulation, similar to \eqref{eq:comp_constr}, using $\bar{c}$ and $\lambda$, since $\bar{c}$ is not orthogonal to $\lambda$, as shown in the figure above. To get around this issue, we slightly modify $\bar{c}$ as follows:
\[\hat{c} = \bar{c} + \begin{bmatrix} 0 \\ \mu \Vert c_{T, t+1} \Vert_2 \end{bmatrix}.\]Then, a compact formulation can be expressed as
\[\begin{equation} \label{eq:compact_form} K_{\mu} \ni \lambda \perp \underbrace{ \begin{bmatrix} c_{T, t+1} \\ \frac{1}{\Delta t} \phi(q_{t}) + c_{N, t+1} + \textcolor{blue}{\mu \Vert c_{T, t+1} \Vert_2} \end{bmatrix}}_{\hat{c}_{t+1}} \in K^*_{\mu}, \end{equation}\]where $K^*_{\mu}$ represents the dual cone, defined as
\[\begin{equation*} K^*_{\mu} = \left\{ \gamma \in \mathbb{R}^3 \mid \gamma^\top \lambda \geq 0,\; \forall \lambda \in K \right\}. \end{equation*}\]Below, we provide a visual illustration of \eqref{eq:compact_form}.
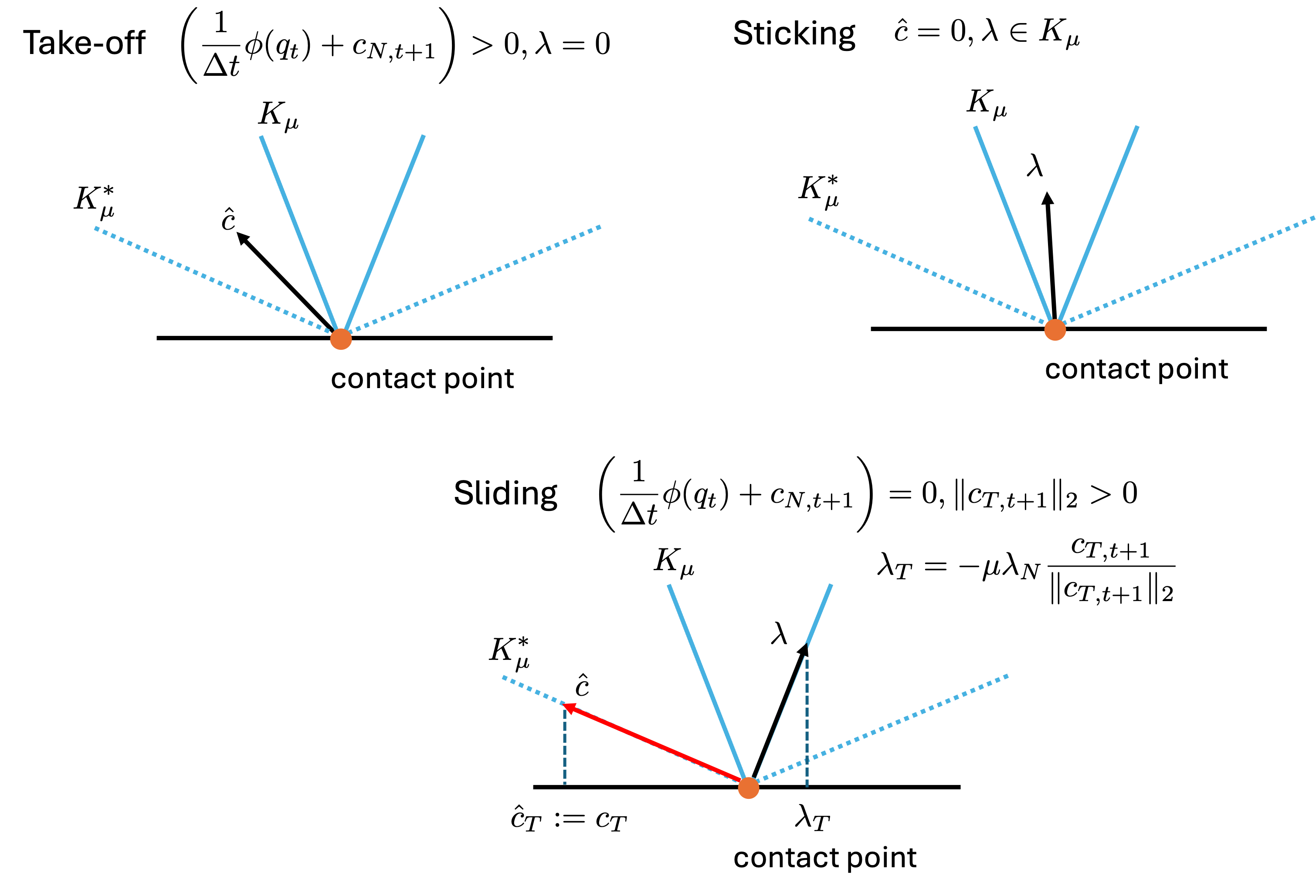
We note that the compact formulation \eqref{eq:compact_form} is related to a Nolinear Complementarity Problem (NCP). It is challenging to solve a NCP in general. Therefore, several approximation methods have been proposed. For example, by relaxing the complementarity constraint, we arrive at a Cone Complementarity Problem (CCP):
\[\begin{equation} \label{eq:CCP} K_{\mu} \in \lambda \perp \bar{c}_{t+1} \in K^*_{\mu}. \end{equation}\]The formulation above is used in MuJoCo, and it can be reformulated as a convex optimization problem. The solution is discussed in a separate blog post. Here, we focus on the potential drawbacks of this approximation. Once again, we visualize the relaxed complementarity constraint.
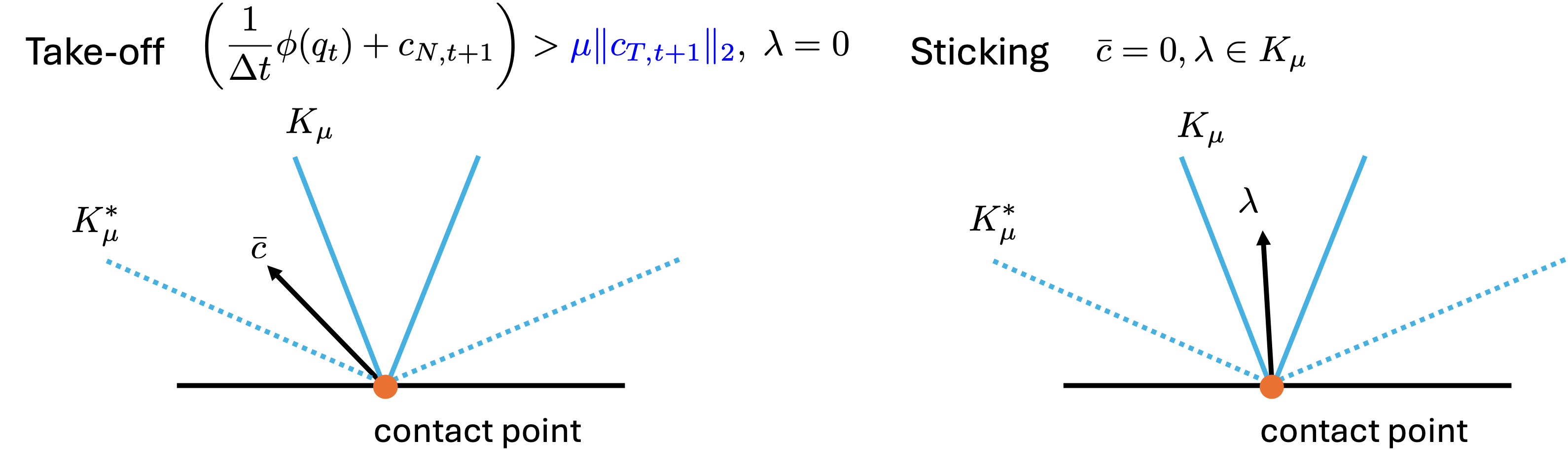
Although there is a difference in the take-off case (highlighted in blue), the CCP in \eqref{eq:CCP} can still model both situations in a reasonable way. However, an issue emerges when considering the sliding case.
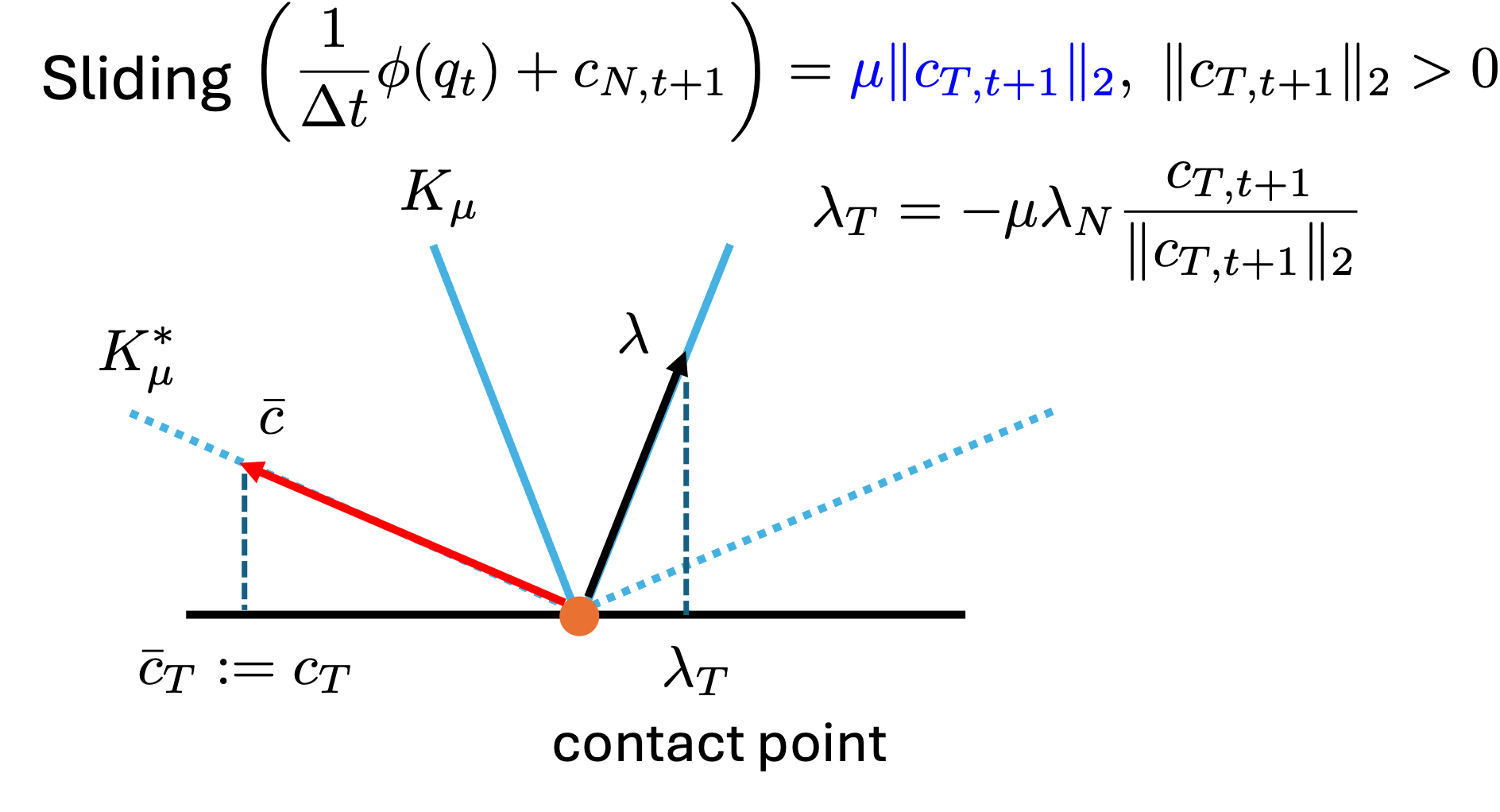
In this model, the term $\left( \frac{1}{\Delta t} \phi(q_{t}) + c_{N, t+1} \right)$ does not vanish. The normal velocity and normal force are both nonzero at the same time, which is physically inaccurate. For example, consider a rigid cube placed on the ground with a nonzero velocity in the x-direction. The cube should slide and gradually slow down due to friction. However, if the CCP model is used, the cube will bounce due to the nonzero normal velocity. Next, let’s see if a similar phenomenon can be observed in MuJoCo. The code for this example is available here.
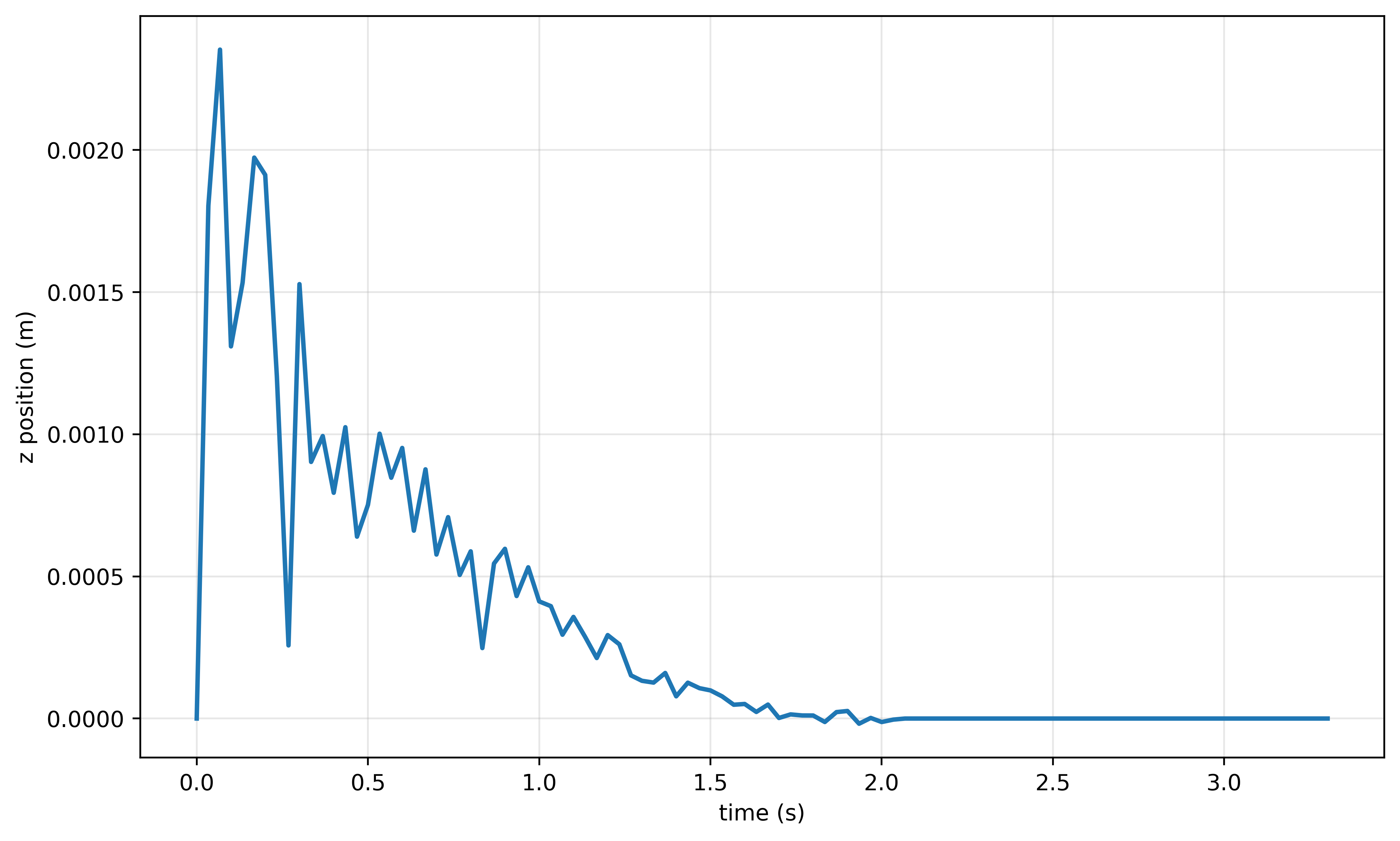
As shown in the figure above, the cube moves in the z-direction, and its displacement from the ground decreases as the tangential velocity $c_T$ diminishes. To conclude, such an artifact only emerges in the case of sliding, and its consequence can be ignored when the discretization step is small and the tangential velocity is low. In robotics applications such as grasping, locomotion, or rolling contact, the sticking mode is often of primary interest and can be precisely modeled using complementarity constraint problems (CCPs).